
Стремление человека приподнять завесу грядущего и предвидеть ход событий имеет такую же длинную историю, как и его попытки, понять окружающий мир. Очевидно, что в основе интереса к прогнозу лежат достаточно сильные жизненные мотивы (теоретические и практические). Прогноз выступает в качестве важнейшего метода проверки научных теорий и гипотез. Способность предвидеть будущее является неотъемлемой стороной сознания, без которой была бы невозможна сама человеческая жизнь.
Понятие “прогнозирование” (от греч. prognosis – предвидение, предсказание) означает процесс разработки вероятностного суждения о состоянии какого-либо явления или процесса в будущем, это познание того, чего еще нет, но что может наступить в ближайшее или отдаленное время.
Прогноз по своему содержанию более сложен, чем предсказание. Он, с одной стороны, отражает наиболее вероятное состояние объекта, а с другой – определяет пути и средства достижения желаемого результата. На основе полученной прогнозным путем информации по достижению желаемой цели, принимаются определенные решения.
Необходимо отметить, что динамика экономических процессов в современных условиях отличается нестабильностью и неопределенностью, что затрудняет применение традиционных методов прогнозирования.
Модели экспоненциального сглаживания и прогнозирования относятся к классу адаптивных методов прогнозирования, основной характеристикой которых является способность непрерывно учитывать эволюцию динамических характеристик изучаемых процессов, подстраиваться под эту динамику, придавая, в частности, тем больший вес и тем более высокую информационную ценность имеющимся наблюдениям, чем ближе они расположены к текущему моменту времени. Смысл термина состоит в том, что адаптивное прогнозирование позволяет обновлять прогнозы с минимальной задержкой и с помощью относительно несложных математических процедур.
Метод экспоненциального сглаживания был независимо открыт Брауном (Brown R.G. Statistical forecasting for inventory control, 1959) и Хольтом (Holt C.C. Forecasting Seasonal and Trends by Exponentially Weighted Moving Averages, 1957). Экспоненциальное сглаживание, как и метод скользящих средних, для прогноза использует прошлые значения временного ряда.
Сущность метода экспоненциального сглаживания заключается в том, что временной ряд сглаживается с помощью взвешенной скользящей средней, в которой веса подчиняются экспоненциальному закону. Взвешенная скользящая средняя с экспоненциально распределенными весами характеризует значение процесса на конце интервала сглаживания, то есть является средней характеристикой последних уровней ряда. Именно это свойство и используется для прогнозирования.
Обычное экспоненциальное сглаживание применяется в случае отсутствия в данных тренда или сезонности. В этом случае прогноз является взвешенной средней всех доступных предыдущих значений ряда; веса при этом со временем геометрически убывают по мере продвижения в прошлое (назад). Поэтому (в отличие от метода скользящего среднего) здесь нет точки, на которой веса обрываются, то есть зануляются. Прагматически ясная модель простого экспоненциального сглаживания может быть записана следующим образом (по представленной ссылке можно скачать все формулы статьи):
Покажем экспоненциальный характер убывания весов значений временного ряда – от текущего к предыдущему, от предыдущего к пред–предыдущему и так далее:
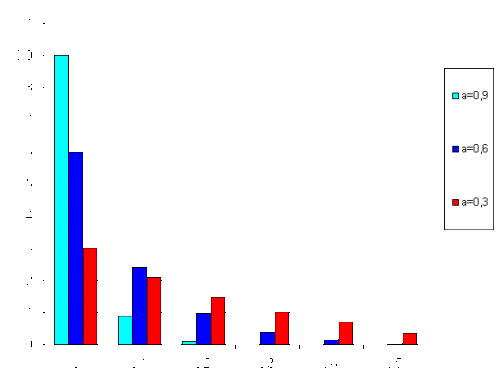
Следует заметить, что значение сглаживающего параметра не может равняться 0 или 1, так как в этом случае сама идея экспоненциального сглаживания отвергается. Так, если альфа равняется 1, то прогнозное значение Ft+1 совпадает с текущим значением ряда Хt, при этом экспоненциальная модель стремится к самой простой “наивной” модели, то есть в этом случае прогнозирование является абсолютно тривиальным процессом. Если альфа равняется 0, то начальное прогнозное значение F0 (initial value) одновременно будет являться прогнозом для всех последующих моментов ряда, то есть прогноз в этом случае будет выглядеть в виде обычной горизонтальной линии.
Тем не менее, рассмотрим варианты сглаживающего параметра, близкие к 1 или 0. Так, если альфа близко к 1, то предыдущие наблюдения временного ряда практически полностью игнорируются. В случае если альфа близко к 0, то игнорируются уже текущие наблюдения. Значения альфа между 0 и 1 дают промежуточные результаты. По мнению ряда авторов, оптимальное значение альфа находится в пределах от 0,05 до 0,30. Однако иногда альфа, большее 0,30, дает лучший прогноз.
В целом лучше оценивать оптимальное альфа по исходным данным (при помощи поиска по сетке), а не использовать искусственные рекомендации. Тем не менее, в случае если значение альфа, превышающее 0,3, минимизирует ряд специальных критериев, то это указывает на то, что другая техника прогнозирования (с применением тренда или сезонности) способна обеспечить еще более точные результаты. Для нахождения оптимального значения альфа (то есть минимизации специальных критериев) используется квазиньютоновский алгоритм максимизации правдоподобия (вероятности), который эффективнее обычного перебора на сетке.
Перепишем уравнение (1) в виде альтернативного варианта, позволяющего оценить, как модель экспоненциального сглаживания “обучается” на своих прошлых ошибках:
Из уравнения (3) ярко видно, что прогноз на период t+1 подлежит изменению в сторону увеличения, в случае превышения фактического значения временного ряда в период t над прогнозным значением, и, наоборот, прогноз на период t+1 должен быть уменьшен, если Хt меньше, чем Ft.
Отметим, что при использовании методов экспоненциального сглаживания важным вопросом всегда является определение начальных условий (начального прогнозного значения F0). Процесс выбора начального значения сглаженного ряда называется инициализацией (initializing), или, иначе, “разогревом” (“warming up”) модели. Дело в том, что начальное значение сглаженного процесса может существенным образом повлиять на прогноз для последующих наблюдений. С другой стороны, влияние выбора уменьшается с длиной ряда и становится некритичным при очень большом числе наблюдений. Браун впервые предложил использовать в качестве стартового значения среднее динамического ряда. Другие авторы предлагают использовать в качестве начального прогноза первое фактическое значение временного ряда.
В середине прошлого века Хольт предложил расширить модель простого экспоненциального сглаживания за счет включения в нее фактора роста (growth factor), или иначе тренда (trend factor). В результате модель Хольта может быть записана следующим образом:
Данный метод позволяет учесть присутствие в данных линейного тренда. Позднее были предложены другие виды трендов: экспоненциальный, демпфированный и др.
Винтерс предложил усовершенствовать модель Хольта с точки зрения возможности описания влияния сезонных факторов (Winters P.R. Forecasting Sales by Exponentially Weighted Moving Averages, 1960).
В частности, он далее расширил модель Хольта за счет включения в нее дополнительного уравнения, описывающего поведение сезонной компоненты (составляющей). Система уравнений модели Винтерса выглядит следующим образом:
Дробь в первом уравнении служит для исключения сезонности из исходного ряда. После исключения сезонности (по методу сезонной декомпозиции Census I) алгоритм работает с “чистыми” данными, в которых нет сезонных колебаний. Появляются они уже в самом финальном прогнозе (15), когда “чистый” прогноз, посчитанный почти по методу Хольта, умножается на сезонную компоненту (индекс сезонности).
Автор: Александр Муха
Источник: BusinessForecast.by
